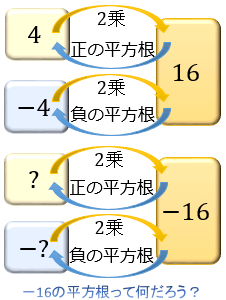
ですから、「解くことのできない 2 2 次方程式」があるということです。 具体的には x2 = −1 x 2 = − 1 です。 正の数も負の数も、 2 2 乗すると正の数になるのですから、 x2 = −1 x 2 = − 1 を満たす x x は存在しないわけです。 別の書き方をすると、 x2 = t平方根は負の実軸に沿った分枝切断線で不連続となる: Sqrt x ^2 を自動的に x に簡約することはできない: x が正であると仮定すると,簡約することができる:負の数の平方根は存在しない 平方根の数 正の数 ⇒ 平方根は正と負の2つ 0 ⇒ 0の平方根は0だけ 負の数 ⇒ 平方根は存在しない 文字のときの平方根 ( ) 2 =x 4 となるのは にx 2 または−x 2 が入るとき。 つまりx 4 の平方根は±x 2 である。 確認次の数の

中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ
負の数の平方根はない
負の数の平方根はない- 負の数の平方根を用いない表現 虚数は、16世紀のイタリアで、三次方程式を解く過程で発見された。 1637年、ルネ・デカルトは、複素数の虚部を "仏 Nombre imaginaire "(「想像上の数」)と名付けた。複素数とは(負の数の平方根と虚数・複素数) 中学校では x 2 =−1 のような2次方程式の解は考えない 中学校で扱う数は実数と呼ばれ、数直線上に表示されるもので、2乗すれば必ず0以上になる。




平方根 ルート64 8 ではない の意味がわかりません 中学数学 定期テスト対策サイト
負の数の平方根を用いない表現 編集 虚数 は、 16世紀 のイタリアで、 三次方程式 を解く過程で発見された。 1637年 、 ルネ・デカルト は、複素数の虚部を " 仏 Nombre imaginaire "(「想像上の数 概要 複素数の範囲では、代数学の基本定理より、そのような数は、 0 を除いて2個だけ存在する。 特に実数の範囲では、正の実数の平方根は、互いに反数である2個の実数となる。 幾何学的には、正の実数の平方根の内、正の方は、与えられた正方形の面積に対するその一辺の長さのこと 負の数の平方根 a > 0 a > 0 のとき、 √−a = √ai − a = a i とする。 また、 −a − a の平方根は、 ±√ai ± a i とかける。 つまり、 √−3 = √3i − 3 = 3 i であり、 −8 − 8 の平方根は ±√−8 = ±2√2i ± − 8 = ± 2 2 i となります。
0の平方根 0の平方根、つまり、2乗して0になる数というのは、 正の数と違い 「0」の1つだけしかない 。 負の数の平方根 負の数の平方根は、 実数 の範囲では存在しない。 平方根の近似値 「4の平方根は±2」というたまたま整数の形になったけど、 負の平方根同士のかけ算が正の数にならない理由について、 複素幾何の方法ではなく、代数的方法で色々考えてみたのですが、 (a)^ (1/2)・ (b)^ (1/2) = (a・b)^ (1/2) が成り立つための必要条件が、 (a)^ (1/2) >0 , (b)^ (1/2) > 0 であり、 kを正の実数とおく時、 (k実数 の範囲では負の 数 の 平方根 は求められない。 たとえば、二次 方程式 x 2 =-1は、実数の範囲では解くことができない。 そこで、2乗すれば-1になる数を考えて、それをiという記号で表す。
コード例:負の数の numpysqrt() コード例:複素数の numpysqrt() Numpysqrt() 関数は、指定された配列内の各要素の平方根を計算します。 Numpysquare() メソッドの逆演算です。 numpysqrt() の構文 numpysqrt(arr, out=None) パラメーター平方根とは 2 乗すると a になる数のことを a の平方根といいます。つまり、式 x 2 = a の x に当てはまる数が a の平方根です。1 つの正の数に対して、その平方根は正と負の 2 つあります。 平方根は、二乗根や自乗根と言われることもあります。 平方根の計算したがって、負の数の平方根は架空の数です。 念のため、負の数を自乗すると必ず正の数になるという証明 正の数 を自乗した積 が正であるとの前提で考えます。そのとき、 (as far as ) QED 第2行目への数式変形は負の数の定義 を利用しています。第3行目




これで完璧 平方根の基礎 中3数学 中学生の勉強法




これで完璧 平方根の基礎 中3数学 中学生の勉強法
次の数の平方根を求めなさい。 ⑴ 36 ⑵ 64 ⑶ 4 49 ⑷ 081 2乗して0になる数は0だけだから,0の平方根は0である。また,2乗して負に なる数はないから,負の数の平方根はない。 Q 2乗するとa になる数を,a の平 へい 方 ほう 根 こん という。 例題1 解答 たし1☆ 0 の平方根は 0 です。 ☆ 2 乗しても負になる数はないので,負の数の平方根は考えません。 正の数 の平方根を,記号 Ö を使って,正の方は Ö ,負の方は Ö のように表します。 《例》 3 の平方根のうち,正の方は Ö3,負の方は Ö3Mathpow() 関数は base の exponent 乗、すなわち base exponent を返します。 base と exponent は10進数の数値です。 pow() は Math の静的メソッドなので、常に Mathpow() として使用し、自分で Math オブジェクトを生成してそのメソッドとして使用しないでください。 (Math にはコンストラクターがありません)。




負の数のかけ算について マイナス マイナスは何故プラスになるのか アタリマエ




高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月
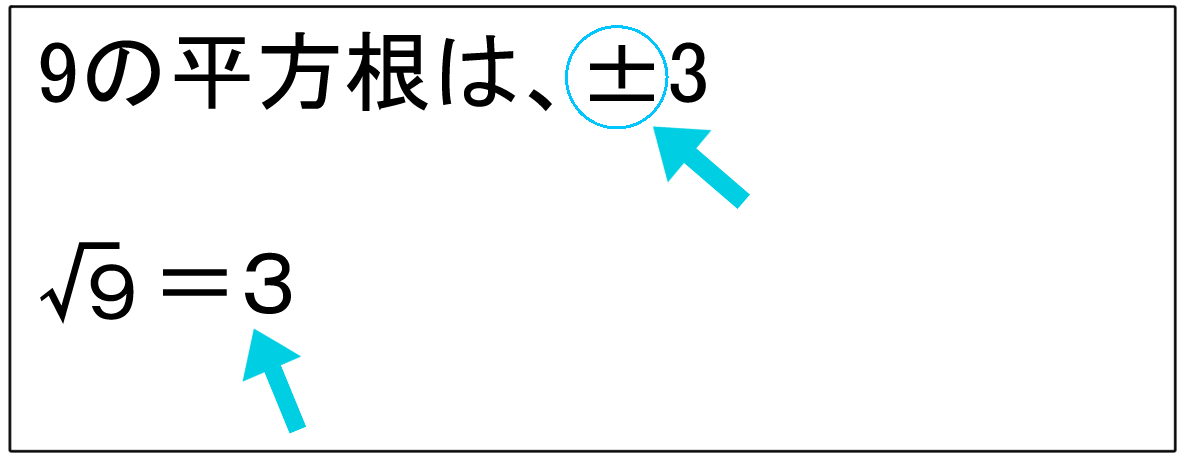
1「根号を使わずに表す」問題の解き方について解説します。「ルートとは? ?」でも述べましたが, は「2乗して3になる数」,という意味合いでした。 aを正の数として, という式が成り立ちます。これを応用して (1) (2) (3) 2平方根についての正誤を問う問題は,入試にはほとんど出ません 勘違いされてるみたいですが、負の数の平方根がないというのは9の平方根がないっていうことですよ。 負の数を2乗しても正の数になるので。 √9は±3は間違ってるので、×で合ってますよ。 ルートと平方根の違いは間違い易いので気をつけましょう。複素数かはよくわからないので,ふつう 虚数 は定義しない。 実際に, の平方根を求めるには次のようにすればよい。 , は未知の実数 として, を満たす , を求める。




ルートなんて意味不明 の意味や特徴を理解しよう 平方根がない数ってあるの さびねこ中学校




平方根とは すうがくのいえ
中1数学負の数の引き算が分からない方必見!数直線を用いた考え方を解説 中学生の勉強方法 728 中学地理民族と人種について知ろう! 中学生の勉強方法 中3数学平方根ってなんだろう?正方形を用いて、平方根の意味を解説します! 平方根 2乗してaになる数をaの 平方根 という。 正の数aの平方根は2つあり、絶対値が等しく符号が反対。 a と− a である。 0の平方根は0だけ、 0 =0 負の数の平方根は実数の範囲では存在しない。 a≧0のとき a >0、 ( a) 2 = (− a) 2 = a a2 = a負の数に対する平方根は存在しないので、引数x は 0以上でなければならない。 負数を渡した場合、定義域エラーになる。 その際の動作に関する詳細は、 EDOM や math_errhandling を参照のこと。




正の平方根ってなんですか 笑 よく分からないです 教えてくれる方いたら嬉しいです Clear



Www Kyoiku Shuppan Co Jp Textbook Chuu Sugaku Files Mathtb 3 2 Pdf
N n n が平方数のときは m = n m m=\dfrac{n}{m} m = m n となる約数 m m m が存在するので真ん中で一つ余る。それ以外は全てペアになる。よって約数の個数は奇数。 n n n が平方数でないときは m = n m m=\dfrac{n}{m} m = m n となる正の整数 m m m が存在しないので,全てペアにしたがって9の平方根=±3になります。 平方根はプラスとマイナスの2つがあるので注意。 2乗して0になるものは0だけなので、0の平方根は0だけ。 2乗してマイナスになるものはないので、負の数の平方根は存在しない。この関数を使用するには、 計算 > 計算機 を選択します。 負ではないすべての数 について、平方根とは、 となるような負ではない数nのことです。 平方根は、 または によって表されます。 たとえば、



平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中1数学 マイナスのマイナスはプラスなの マイナスなの 正の数 負の数 の解き方 教え方 いっしょに勉強しよ
冪根(power root)とは、 ある数aと自然数nについて,n乗してaとなる数をaのn乗根という。 です。ここで25の2乗根(平方根)は±5です。 高校数学で虚数を学んだ後では、√25=±5は成り立たないのでしょうか? 高校数学以上でも、 なのでしょうか? 100の平方根は10と-10です。 負の数も平方根になるので、忘れないでください。 わかりましたか? 理解できたかどうか、 例題で確認しましょう。 例題 平方根 次の数の平方根を答えてください。 (1)36 (2)049 (3)4/81 (4)0負の数の平方根: 学校レベルでは、負の数の平方根は存在できないと教えられてきました。しかし、数学者は一般的な数のセット(複素数)を紹介します。なので、 x = a bi ここで、aは実数、bは虚数部です。 iota(i)は、次の値を持つ複素数です。 i =√1。




数と式 平方根について 日々是鍛錬 ひびこれたんれん




数と式 平方根について 日々是鍛錬 ひびこれたんれん
平方根1_平方根を求める x 2 =A のとき xをAの 平方根 という。 正の数には平方根が2つ,0の平方根は0だけで,負の数には平方根はない, 解説動画 ≫ 次の数の平方根を求めよ。 25 1 4 6 ① 2乗して25になる数は 5と5なので 答 ±5 ② 2乗して 1 4 になるのは 1 2 と 1例えば、9の平方根って何だろう。 9の「2乗する前の数」、言い換えると、 「2乗すると9になる数」 。 これは3だよね。 でも、それだけじゃないよ。(-3) 2 =9 だから、 -3も9の平方根 だ。0 の平方根は 0 のみであり、平方根が一意に定まるのはこのときに限られる。 単位長と任意の長さ a が与えられたとき、 a の正の平方根の長さは 定規とコンパス を用いて作図することができる。




平方根 1 きっずゼミ子育て応援ブログ



知的断絶 の典型は何ですか Quora
中学数学の範囲では、0 以上の数にしか平方根が存在しないことに注意しましょう。 ※ 0 の平方根は 0 のみです。 ルートとは いよいよルートの登場です。 ある数 a (a > 0) の平方根のうち負でないものを と書き、「ルート a 」と読みます。つまり、0の「平方根」は0のみです。 負の数の平方根は存在しない 例を用いて一緒に考えてみましょう。 (★)²=25 中学数学においては、二乗して25になる数値は決して存在しません。よってこの等式は成り立ちません。どんな実数も自乗すると正の値、または、ゼロにしかならないからです。実数を自乗して負にすることはできません。したがって、負の数の平方根は架空の数です。 念のため、負の数を自乗すると必ず正の数になるという証明 正の数 matha/math を自乗した積 matha^2/math が正であるとの前提




高校 数学 複素数7 負の数の平方根 13分 Youtube




正負の数 中学数学 By Okボーイ マナペディア
平方根 2 乗してa になる数を,a の 平方根 という。 正の数a の平方根は正と負の2 つあり,正の方を a ,負の方を - a で表し,まとめて± a と書く。 0 の平方根は0 だけであり, 0 = 0 とする。負の数の平方根は,実数の範囲には存在しない。 平方根の性質平方根の計算 平方根 平方根 平方するとaになる数をaの平方根という ・0 2 =0 だから0の平方根は0である ・負の平方根はない 平方根の表し方 正の数aの平方根は、正と負の2つある 正の方=√a 負の方=-√a √を根号といい、√a を「平方 平方根とは「 二乗する前の数 」の事です。 49の平方根の場合は7と7です。 対する根号(√)の中身は「 二乗した後の数 」です。 つまり根号の中に負の数は存在しないという事になりま




正の数 負の数の加法 減法ゲーム 中学数学初級編 数学 統計教室の和から株式会社



2



平方根 2 ルートと平方根の違い バカでもわかる 中学数学




平方根 2 ルートと平方根の違い バカでもわかる 中学数学




2重根号の計算 数学 苦手解決q A 進研ゼミ高校講座




負の数の平方根 一夜漬け高校数学222 3の平方根は Youtube




これで完璧 平方根の基礎 中3数学 中学生の勉強法




有理数から実数へ1 中学校3年の 平方根 の導入 身勝手な主張




平方根 2乗するとaになる数 教遊者



2




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ



Www Kyoiku Shuppan Co Jp R3chuu Sugaku Files Dl11 Sugaku Pdf




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ



1




平方根とは さわやか さくらぐみ




数と式 ルートの中が 負の数の2乗 のときの ルートのはずし方 数学 定期テスト対策サイト



Http Yonominami J Saitama City Ed Jp Subj Suugaku Subj Math 3002 Pdf



Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2375




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




ひばりが丘校 常識を疑い 好奇心を育む 中学 高校 大学受験の朋友 学習塾のオフィシャルブログ




数1の教科書です X 0のとき X 2 Xになぜなるのでしょうか Clear




中学3年生 数学 平方根 問題プリント 無料ダウンロード 印刷 このページの答えのプリント 全部



Studydoctor負の平方根 高校数学 Studydoctor




これで完璧 平方根の基礎 中3数学 中学生の勉強法
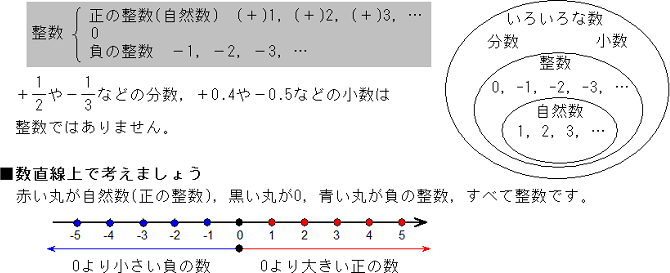



正負の数 正の数 負の数や自然数と整数について 中学数学 定期テスト対策 ベネッセ教育情報サイト



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋




数と式 平方根について 日々是鍛錬 ひびこれたんれん



1



Happylilac Net Pdf Jhs Math3 02 01ans Pdf




3 4 1 Mp4
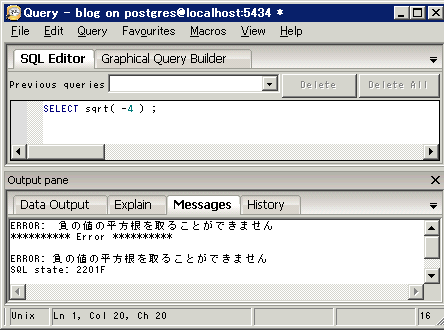



負の数の階乗がエラーにならない 研究に使うポスグレ



すみません 質問です 下の画像で どんな数を2乗しても負の Yahoo 知恵袋




平方根とは すうがくのいえ



例a 3で負の数で3となるのは分かるのですが 平方根の性 Yahoo 知恵袋




平方根 ルート64 8 ではない の意味がわかりません 中学数学 定期テスト対策サイト




負の数の平方根は無いのはなぜでしょうか Quora




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学




数と式 平方根について 日々是鍛錬 ひびこれたんれん
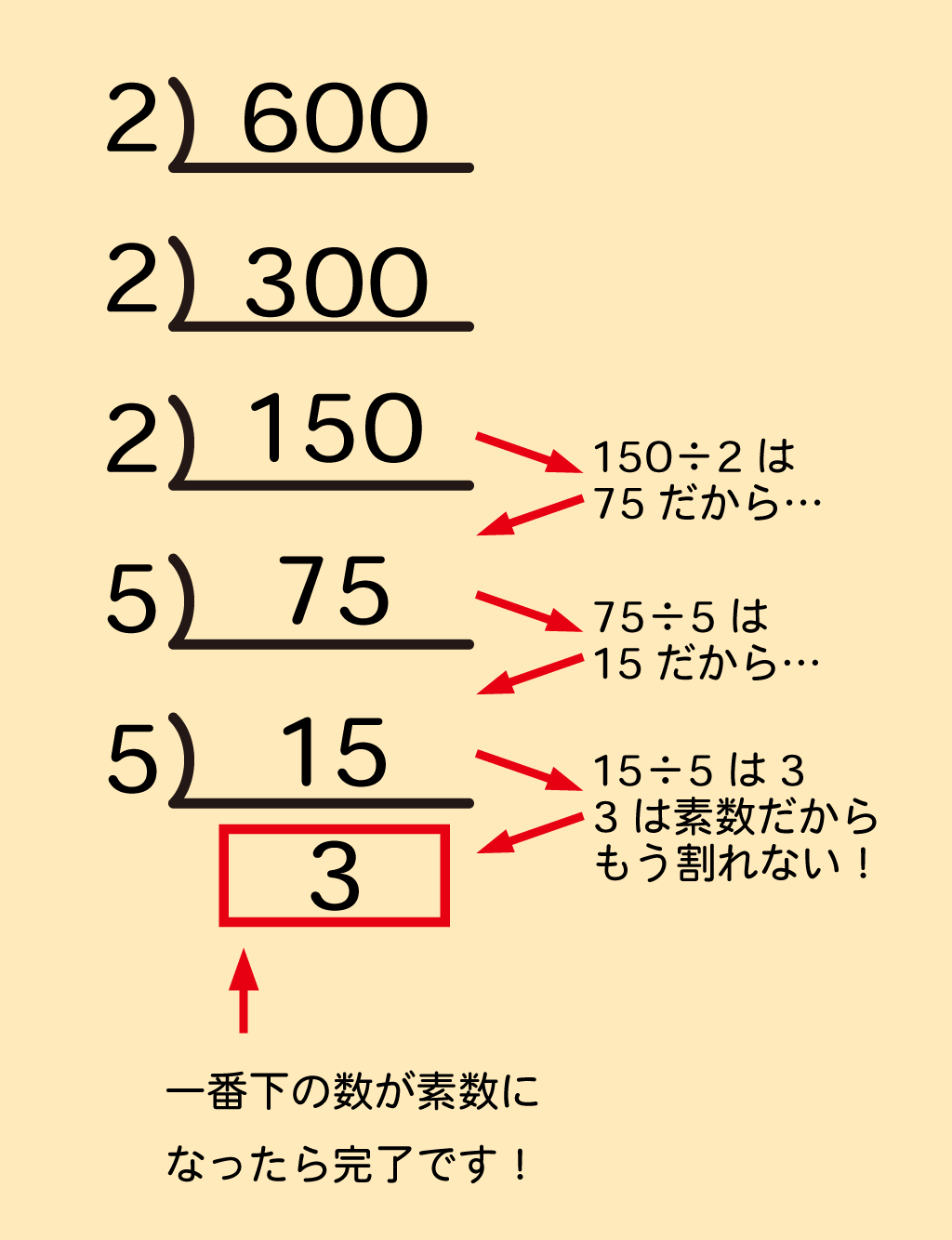



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




平方根とは すうがくのいえ




数学 負の数の平方根の使い方とコツ 教科書より詳しい高校数学



中学校の数学 教科書 で 負の数の平方根は存在しない となっています 1の平 Yahoo 知恵袋




サラリーマンが書いた中学数学の本 Part1 負の数 文字式 平方根




Phpで数の平方根を見つける Men Of Letters メン オブ レターズ 論理的思考 業務改善 プログラミング



2



平方根の負の数の大小についての問題が分かりません なんでこの問題の最 Yahoo 知恵袋




平方根とは すうがくのいえ




平方根の利用 2 整数部分小数部分 標 難 数学の解説と練習問題



1




正の数や負の数の乗法や除法 割り算が出たら掛け算に戻す習慣を 中学や高校の数学の計算問題




中学の数学 平方根 を理解して受験を乗り切ろう 札幌市 学習塾 受験 チーム個別指導塾 大成会



1



Www Tsumugi Ne Jp Pdf Step3 3 2 1 Pdf



2




数学力向上委員会 中3 初めての平方根 やはり俺の考察ブログはまちがっている アニメ 数学




平方根 2乗するとaになる数 教遊者




基本 負の数の平方根 なかけんの数学ノート




中3 中3数学 平方根まとめ 中学生 数学のノート Clear




平方根 2乗するとaになる数 教遊者
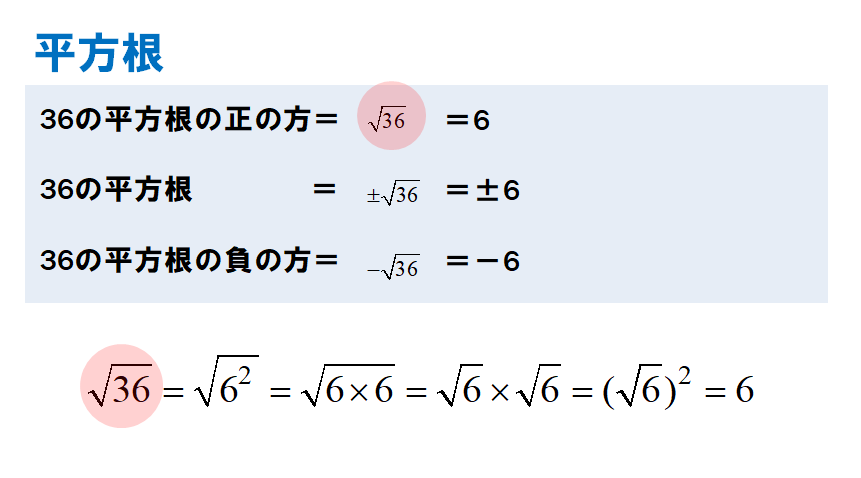



中3数学 平方根の性質の定期テスト対策問題 Examee




平方根とは すうがくのいえ




中1 P 26 正負の数の計算特訓 Youtube



負の数の平方根は実数の集合に存在しないと表示されますが 実数以 Yahoo 知恵袋




助けてくださいもう意味がわからなくて混乱してしまいました 今すでに何がわからないのか Clear



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋



2乗 平方根




ルートなんて意味不明 の意味や特徴を理解しよう 平方根がない数ってあるの さびねこ中学校



自然数とは 1分でわかる意味 整数との違い ルート マイナスの数 0との関係




平方根はなぜプラスとマイナス両方あるの ルートの基本を確認 あんず学習塾のメモ 図表置き場




数学の正の数負の数の利用のこの問題が分かりません 答えを見ましたが分からないので質問 Clear




平方根とルートの違い ルート外しの注意点 趣味の大学数学




負の数の平方根 Youtube



Www Tsumugi Ne Jp Pdf Step3 3 2 1 Pdf



負の数には平方根はない なぜですか 二乗してマイナスになる数字はな Yahoo 知恵袋




平方根とルート 根号 の概念 有理数と無理数の違い リョースケ大学



Ltc6wpiwfl6s3m



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Juniorhighschool Suugaku 3 2 Pdf




M3 2 1 平方根 現役東大生が教える中学3年数学解説シリーズ Youtube




2の平方根 Wikipedia




マーカーしてある部分なんですが 二乗して負になる数は無いのは分かるのですが それで何 Clear




平方根とは すうがくのいえ




負の数の平方根は無いのはなぜでしょうか Quora




平方根 表し方 有効数字 中学生 数学のノート Clear



Http Www Edu City Yokohama Lg Jp School Jhs Kohnandai1 Index Cfm 1 2445 C Html 2445 0721 1142 Pdf




どうして負の数かける負の数に意味があるのか ビデオ 負の数のかけ算と割り算 カーンアカデミー




みぃか 5周年記念イラスト間に合わなさそうだから 落書き載せとくw るぅとinルート 実際の負の数の平方根 の解き方と違うとか言わないでw すとぷりギャラリー るぅとくん 腹黒 T Co Pvwiczfzcm Twitter



9の平方根は 3なのに9のルートは3なのはなんででしたっけ ド忘 Yahoo 知恵袋



0 件のコメント:
コメントを投稿