積分を用いた証明 二つ目の説明です。数学2の知識が必要になります。積分を使って V = 1 3 S h V=\dfrac{1}{3}Sh V = 3 1 S h を証明します。 底面積の形によらない(円錐でも三角錐でも四角錐でも適用可能)証明方法です。 まとめ:円錐の体積の求め方の公式はシンプル 円錐の体積の求め方はどうだったかな?? 底面積×高さ×1/3 という公式は意外とシンプルだったよね笑 最後に1/3をかけることさえ忘れなければ、ぜったいにテストでも間違えないはず。円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S
1
立体の体積の求め方 円錐
立体の体積の求め方 円錐- 高さの分からない円すい展開図! どうやって立体の体積を求めるの? 立体図形 立体図形 次の展開図から出来る円すいの体積を求めなさい 知りたがり 円すいの体積は、底面積 高さ ÷ 3 積分を用いて円錐の体積 を求める以下の公式を導出します. ここで, は底面の半径, は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角をθとすると,この直線は と表せます.この直線の式とx軸および2直線 および で囲まれた図形




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
〇〇錐という立体の体積は底面積×高さ×\(\frac{ 1 }{ 3 }\)と覚えている方も多いと思いますが、\(\frac{ 1 }{ 3 }\)という係数はここの導出過程から出てくるものです。 球 最後に球の体積についてです。半径\(R\)の球の体積を求めてみたいと思います。立体の体積の求め方 これで,円錐の体積が円柱の体積の 三分の一 になっていることが示されたのですが,以上の議論は,「任意の立体について,基準となる軸に対して軸と垂直な平面による切断面の面積が分かれば,その立体の体積を定積分により求めることができる。2章 空間図形 48 140 次の図の立体の体積を求めよ。 ⑴ ⑵ 138 次の図の角錐の体積を 求 めよ 。 ⑴ ⑵ ⑶ 141 右の図のよ う に ,1 辺 12 cm の立方体から,3 点 A ,C ,F を通る平 面で切ってできる 2 つの立体のうち,小さい方の立体を取り除いた。
演習問題に挑戦しよう! 円錐の体積比 まとめ 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか? 三角錐や円錐といった「錐」とは,穴をあける道具のように先の尖った立体です. では,「〇〇錐」の体積の求め方はどうだったかというと, \begin{align*} (\text{〇〇錐の体積}) = (\text{底面積})\times (\text{高さ})\times\frac{1}{3} \end{align*} でした.これは三角錐でもLesson 43 立体の体積 第6章 空間図形 2 右図の円柱の体積を求めなさい。 家庭教師のガンバは、勉強が嫌いな子、勉強が苦手な子、勉強のやり方がわからない子を中心に年以上運営されている家庭教師センターです。
体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱(管) 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方立体の表面積展開図(入試問題) → 携帯版は別頁 == 立体の体積(入試問題) == 要点四角柱,三角柱,円柱の体積 四角柱,三角柱,円柱の体積 V は,底面積 S と高さ h を使って表すことができます. V=Sh 特に,円柱については,底面の半径が r 円錐の体積の求め方 円錐の形は? 円錐とは、以下のようなとんがり帽子の形の図形を言います。一般的に、「錐」という表現がされる場合には、頂点がとがった形のものを指します。 円錐の体積公式について




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
三角柱の体積の求め方は 「底面積 × 高さ」でしたね。 底面積は 4 × 4 × 1 2 = 8 よって、三角柱の体積は 8 × 8 = 64 体積は 64( c m 3 ) となります。 続いて、 三角柱の表面積の公式は 「底面積 × 2 側面積」でしたね。 すると、底面積は先に求めた 8 c m 2角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 メニュー円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




中3 三角形の相似 円錐の体積比 日本語版 Youtube
小学6年生の算数 角柱や円柱の体積の求め方・公式 問題プリント ツイート 無料ダウンロード・印刷できる、角柱・円柱の体積を求める練習問題プリント です。 角柱や円柱の名前、体積を求める公式を確認し、体積の計算をする練習を繰り返し行う この記事の目的:錐形を求める際に「3分の1」する理由を中学生にも分かるように説明する. はじめに 錐形は3分の1 指針 ①特別な四角錐を考える ②特別な三角錐を考える ③錐体の体積の求め方の根本を考える ④体積が変わると? 最後に 回転体の体積、表面積の求め方 次の図形を直線を軸として1回転してできる回転体の体積、表面積を求めなさい。 正方形、長方形を回転させると円柱ができます。 つまり、上の図のような円柱の体積、表面積を求めれば良いということになります




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




円錐の表面積の求め方 公式と計算例
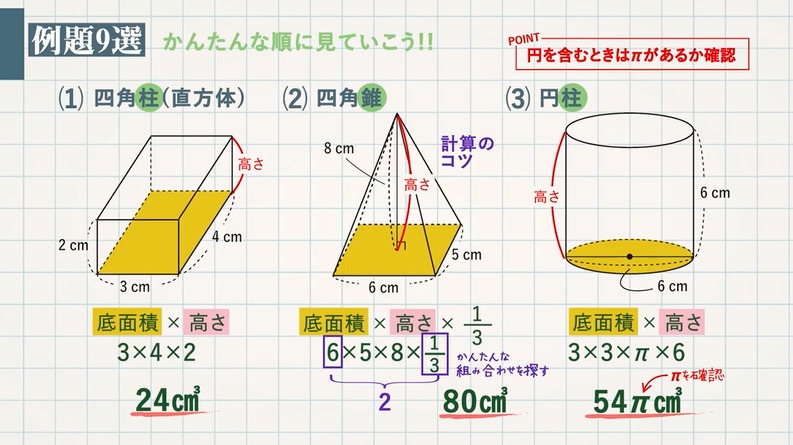
突然ですがみなさん、錐の体積の求め方はご存知ですか? 底面積が半径aの円である円錐を横に並べて、ふたつの立体図形を見比べてみましょう。 そして、求めたい円錐の体積は、さっき体積を求めこの立体の体積は (cm 3 ) 外側の体積 160π (cm3)から空洞になっている内側の体積 40π (cm3)を引くと V=1π (cm3) 大きな円錐の体積は π×6 2 ×10÷3=1π (cm3) 上端の円錐の底面の半径 ( x とおく)は,比例(相似)の関係を使って求めることができる.縦:横 x 5x=106立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学




角錐 円錐の体積と表面積の公式 数学fun
立体角の計算例 円錐の立体角は、 2 π ( 1 − cos θ 0) という公式で計算することができます。 ただし、 θ 0 は円錐の中心軸と母線がなす角度(平面角)です。 円錐の底面を円板をみなせば、「円板が張る立体角の公式」と言うこともできます。(体積の計算) 立体の体積を求めるには,体積の微分が断面積になることを利用します. すなわち,左端 a から座標 x までの区間にある体積を x の関数として V(x) で表し, x における断面積を S(x) とおきます. 上で復習した面積の求め方と同様にして 今回は、円錐(えんすい)の体積の求め方(公式)について書いていきたいと思います。 // 円錐の体積の求め方公式 円錐の体積を求める問題 問題① 《円錐の体積の求め方》 問題② 《円錐の体積の求め方》 問題③ 《円錐の高さの求め方》 問題④ 《色のついた立体の体積の求め方》



双円錐 Wikipedia




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




角柱 円柱の表面積と体積の公式 数学fun



円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




角錐 円錐の体積と表面積の公式 数学fun




計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



円錐 体積の比較 中学から数学だいすき




円錐の体積の求め方 公式 小学生 中学生の勉強




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



下の図の円すいと円柱を合わせた立体の体積を求めなさい なお 円周率はpを用いる Yahoo 知恵袋




三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学



1




三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ




円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ




表面積と体積の比の問題 立体の相似比を出すのが一番最初だ 中学や高校の数学の計算問題




円錐の体積の求め方 公式と計算例




中学数学 円錐の裏技集 暗算で中心角 側面積 表面積 中1数学 Youtube




体積の求め方 計算公式一覧




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学



1




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 回転体の体積 表面積を求める問題を解説するぞ 中学数学 理科の学習まとめサイト



1



円錐とは 体積 表面積の公式や求め方 受験辞典




高さの分からない円すい展開図 どうやって立体の体積を求めるの




立体の体積を求める問題 回転させてできる立体 苦手な数学を簡単に



3




中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




空間図形14 円すい台の体積 Youtube
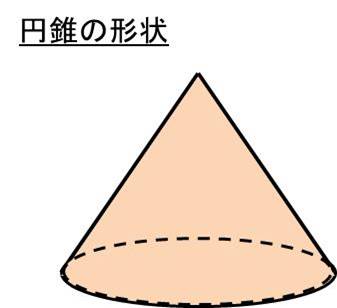



円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん



この問図形の表面積と体積を教えてください 上の円錐と円柱 Yahoo 知恵袋




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者



次の図は 大きな円錐から小さな円錐を切り取ったものです 次の問いに答えなさい Yahoo 知恵袋




円錐の体積ってなんであの公式なの Webty Staff Blog




円錐や角錐の体積の求め方 中学1年数学 Youtube




回転体の体積と表面積 中学数学の計算の求め方 リョースケ大学




体積比の求め方が分かりません Clearnote
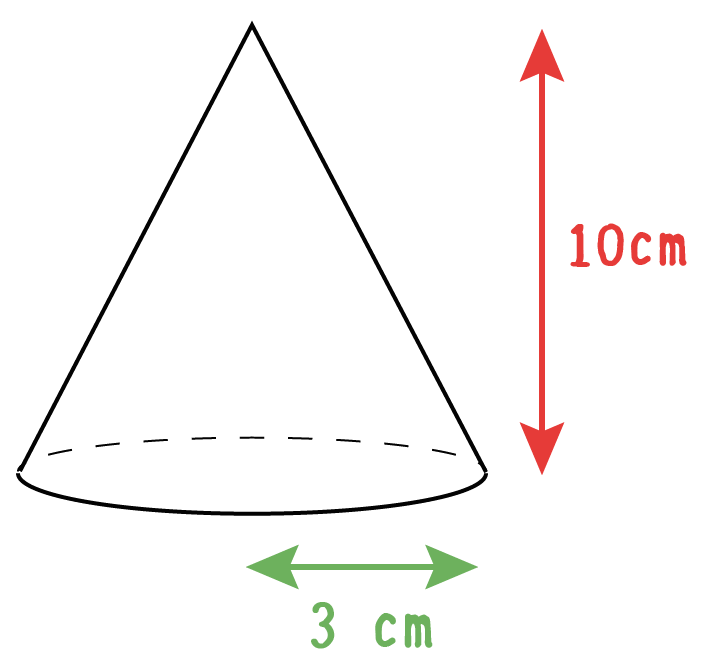



計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




この体積の求め方を教えてください Clearnote




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




毎日問題を解こう 26 苦手な数学を簡単に



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者




球の表面積と体積の公式 数学fun




円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




角錐 円錐の体積と表面積の公式 数学fun



6 17 第6章 空間図形立体の表面積と体積 円錐の表面積 ユニバーハイスクール 高3




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



地図の体積計測



このような円錐を2つくっつけた立体の体積の求め方をお願いします 式だけ Yahoo 知恵袋




円錐の表面積 Youtube




円錐の体積を求める Youtube



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋



積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典




高さの分からない円すい展開図 どうやって立体の体積を求めるの




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




立体の表面積の求め方 直方体 円錐 円錐台 バカでもわかる 中学数学
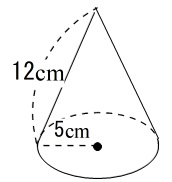



円錐 すい の表面積や四角錐 五角錐の体積の求め方




円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ




円錐の体積ってなんであの公式なの Webty Staff Blog



円錐とは 体積 表面積の公式や求め方 受験辞典




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




体積の求め方 計算公式一覧



Studydoctor円錐や角錐の体積の求め方 中学1年数学 Studydoctor



円錐とは 体積 表面積の公式や求め方 受験辞典




立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




高さの分からない円すい展開図 どうやって立体の体積を求めるの




3分でわかる 円錐の体積 表面積の求め方 合格サプリ



立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者




21番は高さの求め方 22番は母線の求め方を教えてほしいです Clearnote




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1 数学 中1 立体の表面積 Youtube




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




相似と体積比 3 ネット塾



図のような円錐台の体積を求めるにはどのような計算をすればよいか教えてください Yahoo 知恵袋




空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト




中1 中1 数学まとめ 立体の体積や表面積など 中学生 数学のノート Clearnote
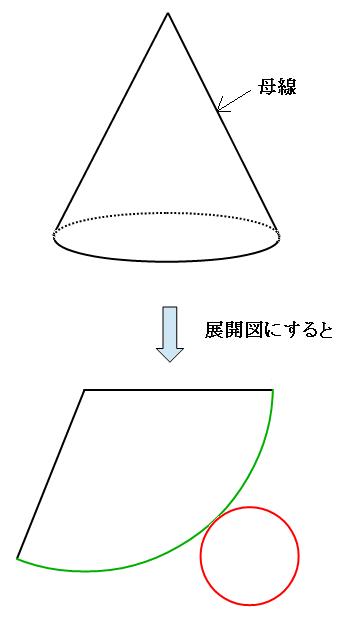



円錐の表面積の求め方を解説 円錐の表面積の求め方は完全パターン化できる




円錐の表面積 Youtube




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室
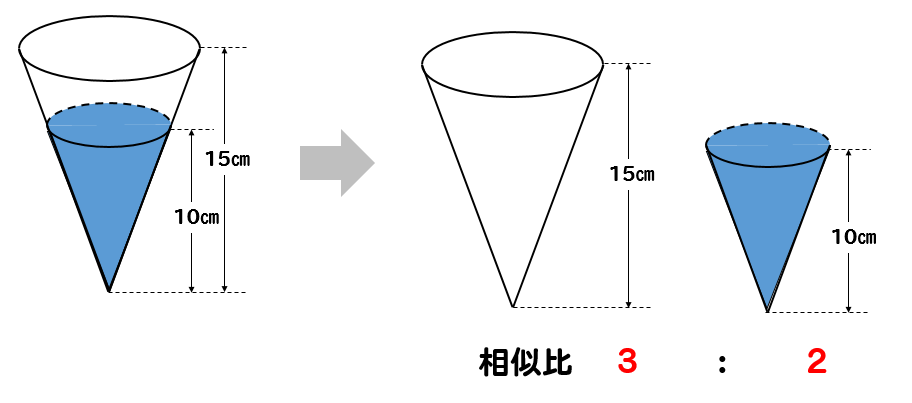



中学数学 円錐の体積比を相似を使って求める方法を問題解説 数スタ




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学




中学1年生 数学 空間図形 立体の体積と表面積 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




角錐 円錐の体積と表面積の公式 数学fun




19年前期 千葉県公立高校入試 数学 第5問 文章題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




中1数学 円柱 円すいの表面積の求め方がサクッとわかる 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿