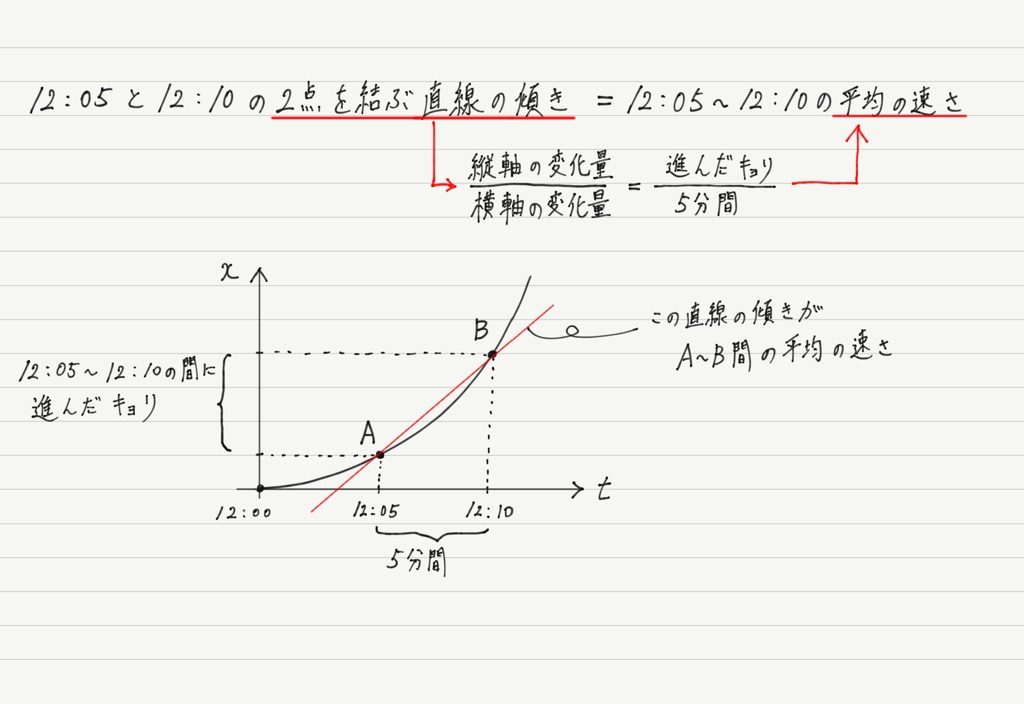
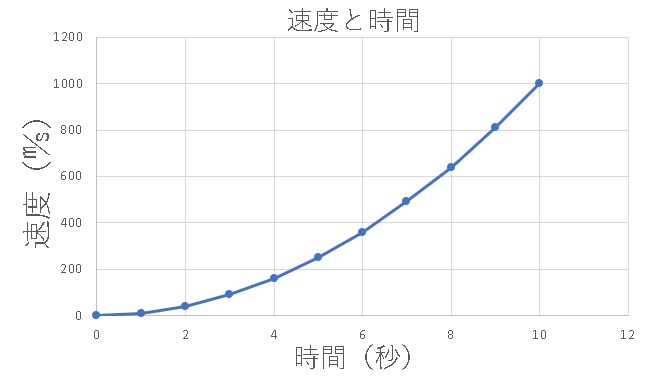
平均の速さ:変化の間、同じ速さで走ったとみなしたときの速さ 瞬間の速さ(速さ):時々刻々と変化していく速さ 速さの定義式で説明すると、 0に限りなく近い時間で起きた変化で考える場合は瞬間の速さ、それ以外は平均の速さ です。 速度の定義式る時間は比例することから、計算によって地震伝わる速さと距離、時間の 関係を計算によって求める。 上のグラフは、兵庫県南部地震における彦根市と福井市での揺れの大きさ と震源からの距離、P波とS波が届くまでの時間をグラフで表したものでXtグラフの傾きが速さを表す というのは重要なポイントです。 傾きが急なグラフほど,速いスピードで運動していることになります。 ② vt グラフ 続いて,v(速さ)とt(時間)のグラフ(vtグラフ)です。 これは「時間が経つと速さはどう変化するのか?
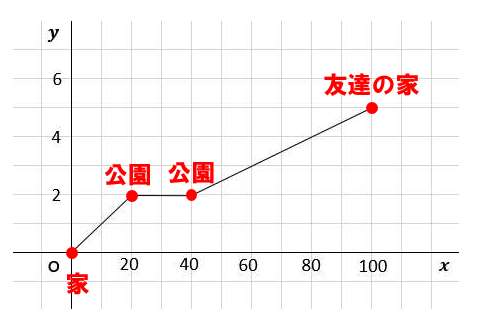
中2数学 一次関数の利用 文章題 歩く距離と時速のグラフ問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
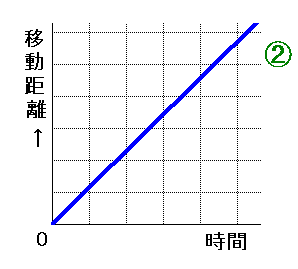
速さと時間の関係 グラフ
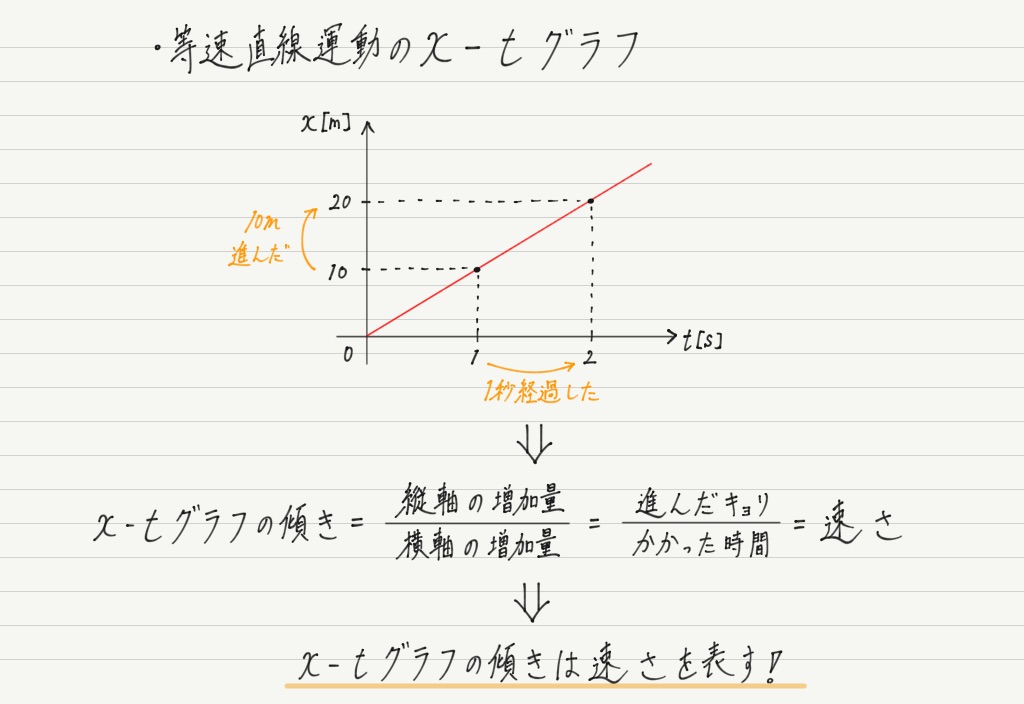
速さと時間の関係 グラフ- すなわち、 x=∫atv(0) dt=(at^2)/2v(0)tx(0) です。x(0)は物体が運動を開始した場所です。 さて、tはこの二つの式の関数ですから、グラフで表すと、時間と速度の関係は1次関数、時間と移動距離の関係は2次関数になっています。速さと比 (旅人算の基本) では進行グラフの基本的な使い方を確認しましたが,このページでは進行グラフそのものを問題としている代表的なパターンを紹介します. まずは1問目です. 問題1:下のグラフのように,AとBの間を2台の車P,Qが一定の速さで



1
中学物理の質問です 斜面を下る物体の 時間と速さとの関係を表したグラフはアイウのうちどれか。 という問題なのですが 答えはイでした。 これはつまり、比例しているということですよね? でも、斜面を下る物体の速さはだんだん速くなると習いました。位置と時間の関係のグラフから私たちが何を読み取れるか見てみましょう。 If you're seeing this message, it means we're having trouble loading external resources on our websiteした「速さ」の導入指導においては,変数の選 択や変数間の関係の吟味を行ったり,比例関係 という仮定を意識したりすることが重要とな る。さらに,本導入授業では,グラフ電卓に示 されたグラフやデータから「速さ」の関係式の 導出まで目指している。
進んだ距離を速さととらえている。または,変化の割合の理 解が不十分でグラフ上の座標(2, 00)の 座標をそのま ま答えている。 誤答例2(毎分)0(m)「速さ=距離×時間」ととらえている。 設問⑵ 正答 (毎分)0(m)グラフと速さ(国府台女子学院中学部 10年) グラフを読み取る力(桜蔭中学 11年) 時間と速度の関係グラフ(立教女学院中学 10年) へだたりと時間のグラフ(明治大学付属明治中学 11年) 点の移動と面積関係(洗足学園中学 11年) 学校、A地点、B地点、公園(筑波大学附属駒場中学 08年) 今年、13年の桜蔭中学の入試問題(桜蔭中学 13年) 山上りとこれらを直線で結べばグラフの完成です。 比例・速さ 一定の速さで、進む問題も、比例の定番中の定番です。 例題2 兄は自転車に乗って、弟は徒歩で、家を同時に出発し、家から \(10m\) 離れた駅に
そして、冒頭でも話した通り、波の式は 3ステップ で作ることができます。 波の式の作り方! ( y − x ) グラフは ( y − t ) グラフに書き換える! ある1点の単振動を時間の関数で表す が位置 x に届くのにどれくらいかかるか考える それでは、実際速さは,時間と道のりの2つの量の割合で表すことができます。 このことを数学的に述べると,次のようになります。 例えば,運動しているある物体について,時間の基準を適当にとり,時刻t 1 (秒)にAの位置にあったものが時刻t 2 (秒)にBの位置にきたとします。前回の記事ではこんなグラフが登場しました。 一定の加速度で加速している場合の距離と時間の関係です。 赤のグラフがx=2t 2 青のグラフがx= (1/2) t 2 グラフ上の矢印の傾きは、その時刻での速さだということをお話しましたね。



グラフから速さを求める 中学から数学だいすき



要点チェック一問一答 物体の運動
進研ゼミからの回答 (道のり)=(速さ)×(時間)が成り立つので,一定の速さで進む場合,(時間x)と(道のりy)の関係は1次関数になり,グラフに表すと直線になります。 座標(x, y)は,いつ(x),どこ(y)にいるのかということを表し,一定の速さで進むので, 直線の傾きは速さを表しています。 下図に、物体Aの位置 x mと時刻 t sの関係を表す x – t グラフと、物体Bの速度 v m/sと時刻 t sの関係を表す v – t グラフを示した。 (1)物体Aについて、 t =10 s、 t =30 s、 t =60 sでの位置( x 座標)と速度を求めよ。 「道のり=速さ×時間」になっています。 (2)の解説 図を見て、時間が÷4になっているので、道のりも÷4します。したがって、 =3÷4= (時速)80(km) です。「速さ=道のり÷時間」になっています。 (3)の解説 比例では、縦に並んだ数字にも規則性があります。




至急 中3理科 瞬間の速さの問題です 多分やり方を知っている方な 物理学 教えて Goo




B 時間と移動距離の関係のグラフが なぜ右上がりになるのかわかりません A Clearnote
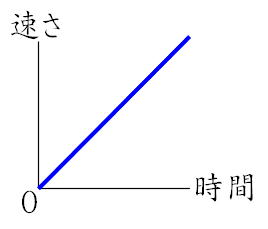
「速さ」と「速度」の違い 一言で言い表すと、「速度」=「速さ」+「向き」ということになります。 「 速さが一定 」と言われると、 どんな向きで動いていてもスピードが一定ならok です。 でも、「 速度が一定 」だと、 方向もスピード両方が一定 でなければいけません(下図参照) x=vt (変位=速さ×経過時間)の公式から 、 グラフの面積部分が移動距離x を示します。 グラフの線が縦軸vの正にあるか負にあるかが、かなり重要です。 時間 (横軸)は、(一定の距離を見つけ) 速さと時間が逆比 になる こちらでも解けます。 だろうは90km行くのに3時間、びばりは同じ距離を1時間半ですから、 かかった時間の比は「だろう(3)2:びばり〔15〕1」です。
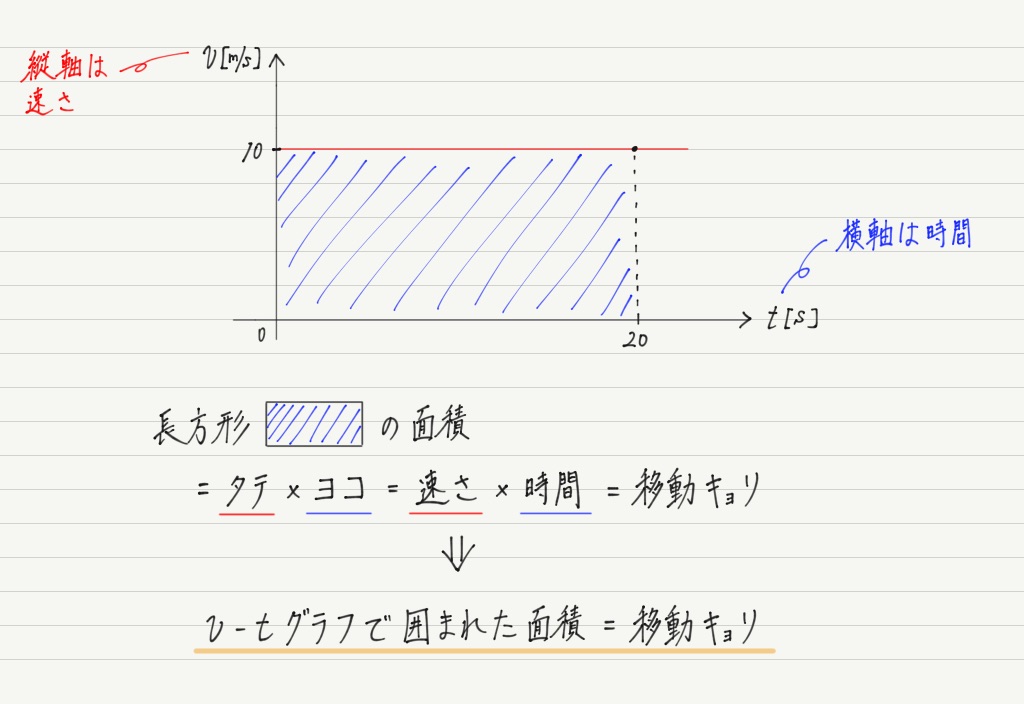



等速直線運動のグラフ 高校物理をあきらめる前に 高校物理をあきらめる前に



1
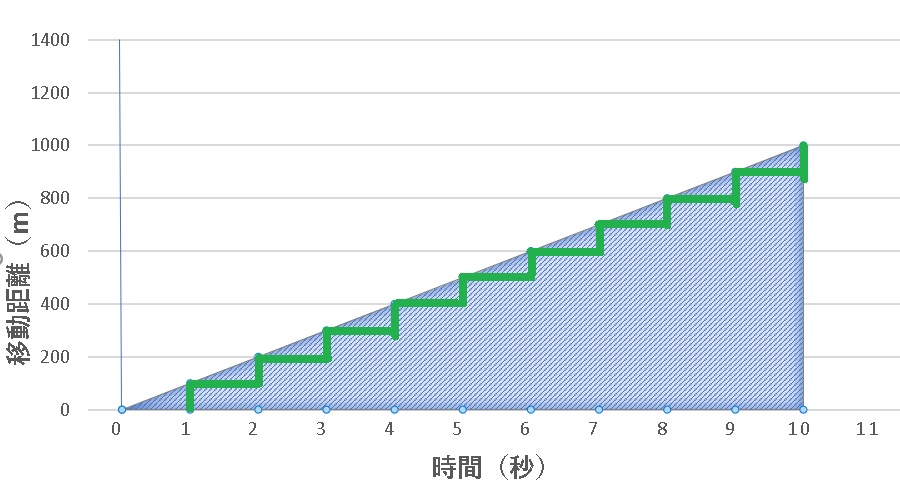
速度vと時間tの関係を表したv−tグラフについて解説していきましょう。 等速直線運動のv−tグラフは、v(速度)がずっと一定 下の図のグラフは、 縦軸を速度vm/s、横軸を時間ts としたもので、 v−tグラフ といいます。なので, 位置と速度の関係 をよく理解してもらったあとで, そのアナロジーを用いて加速度の議論を行うことにする 1 物理量の諸関係式を単に公式で与えずに, 数学的な構造まで明確にして記述する利点はこのようなところにある Continue reading 速度と時間のグラフといっても移動距離と時間のグラフです。 縦軸は経過時間横軸は移動距離を表しています。 グラフの傾きは一定です。 緑の線を記入しましたが、1秒間で100メートルずつ移動したことになります。 パット見100㎧ですが 速度 距離 時間 速度は上記の式になります。 式を入れ替え変更すると VT=M → M距離=速度V*時間T



速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に




物体の運動
速さの単元で出てくる主な単位換算 1km=1000m 1 k m = 1000 m 1 1 分 =60 = 60 秒 1 1 時間 =60 = 60 分 =3600 = 3600 秒 分速 = = 秒速 ×60 × 60 時速 = = 分速 ×60= × 60 = 秒速 ×3600 × 3600 これらも丸暗記する必要はなく、ほとんどは自然と導出できると思います。 距離の換算は以前説明しましたが、基本単位である m m (メートル)の前につくアルファベット m m 、 c反応の速さは,濃度が大きいほど,また温度が大きいほど,大きくなることを指摘できる。 グラフから,測定していない温度における反応時間を予想できる。 ・触媒の有無も反応の速さに影響することを説明する。 反応の速さの実験は手間がかかるので 図9 波の速さ そうすると、波の速さ v = \(\frac{10 m}{50 s}\) =0 m/s(メートル毎秒)ですね。 波の速さについて、物理学的な表し方をしてみましょうか。 波源が1回振動すると、波は1波長分進みますね。 つまり、時間が周期 T s経つと波は波長λmだけ進む



3



実戦問題3年 物体の運動
みはじの計算 「みはじの計算」とよく言われますが、「道のり (距離)」と「速さ」と「時間」の関係を表したもので、今まで多くの小・中学生と勉強をしてきましたが、全員が知っているというかなりメジャーなものになっています。 ・道のり=速さ×小学生の算数 変化と関係・データの活用(数量関係) 練習問題プリント 無料ダウンロード・印刷 小学5年生 速さ・時間・道のり 練習問題プリント お気に入り
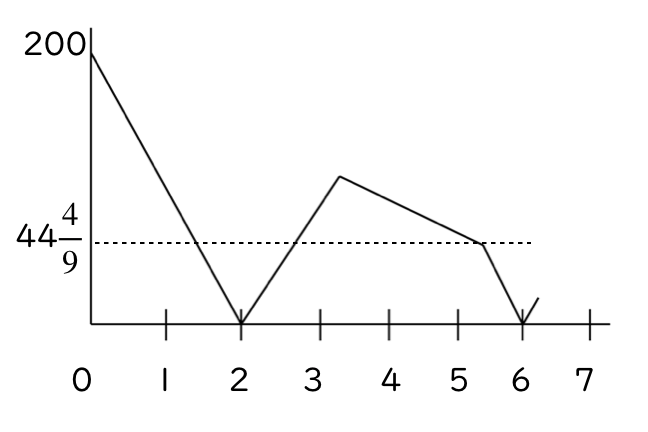



2人の間の距離のグラフ 芝 H19 大問9




平均の速さは変化の割合 傾き 永和進学ゼミ 個別指導ソフィア 学習塾ブログ




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




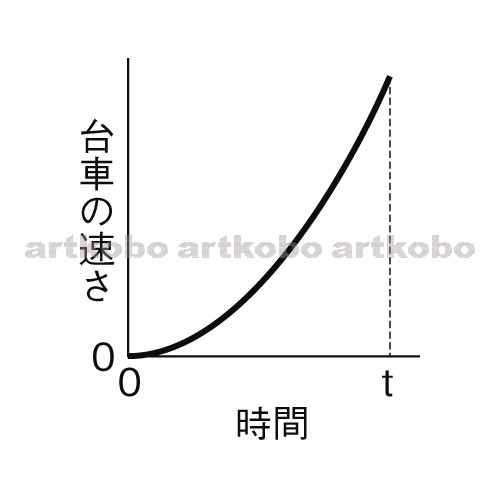
中3です このグラフはなぜ台車の速さを 表していると言えるのですか Clearnote



Makasaka S Homepage 高校ぶつり実験 時刻表の解析




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




中3理科 速さの計算 映像授業のtry It トライイット
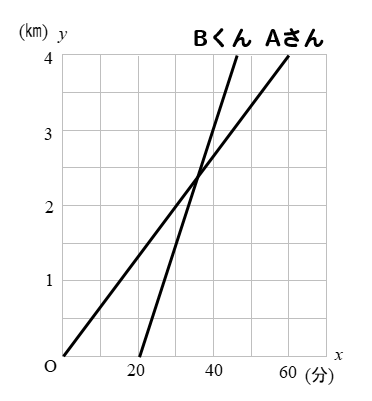



一次関数の利用 追いつく速さの文章問題を解説 数スタ
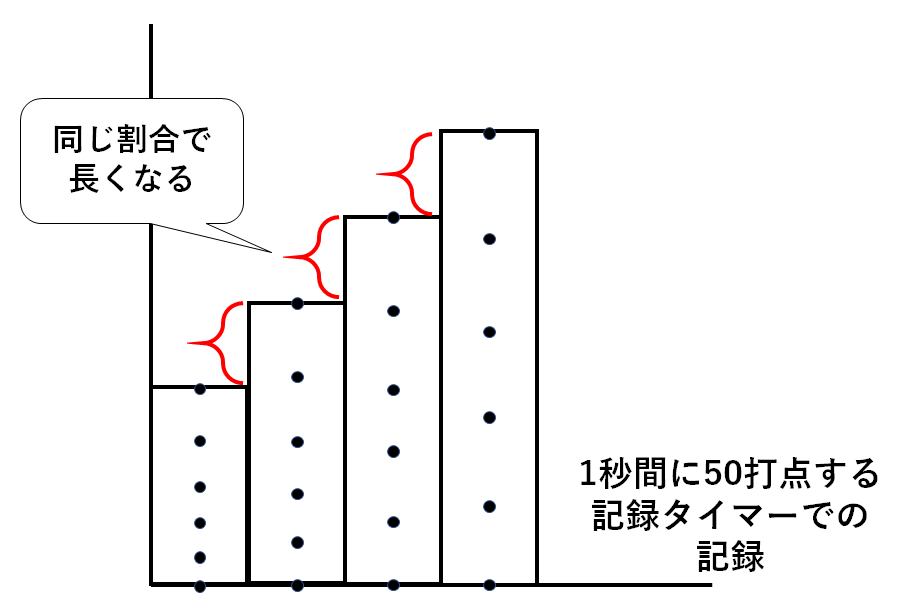



中3物理 いろいろな運動 中学理科 ポイントまとめと整理



19 力学 Kondolab



Adoko 中三物理28年度 第3章仕事とエネルギー



速さと加速度2 文系でも分かる数学講座



大至急お願いします 中3理科の斜面を下る台車の運動の実験の考察で Yahoo 知恵袋




高校物理 運動エネルギー 練習編2 映像授業のtry It トライイット
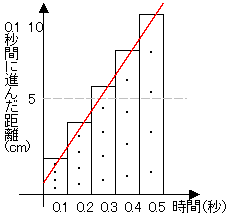



運動と力 Hello School 中学理科 ハロ理科 No 13
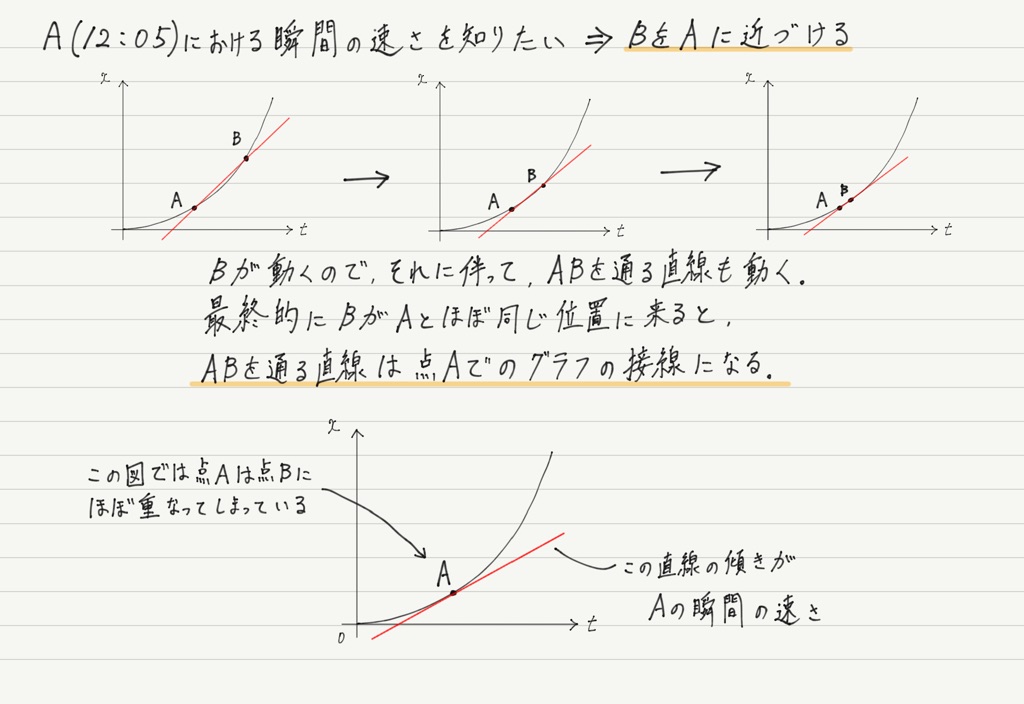



速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に




物体の運動




問題のやり方を教えてください 至急お願い致します Clearnote



中3理科です 物体が斜面を下るとき 速さと時間は比例する 移動距 Yahoo 知恵袋




高校物理 v tグラフ 映像授業のtry It トライイット




Web教材イラスト図版工房 R C1m 時間と速さのグラフ 1




物体の運動
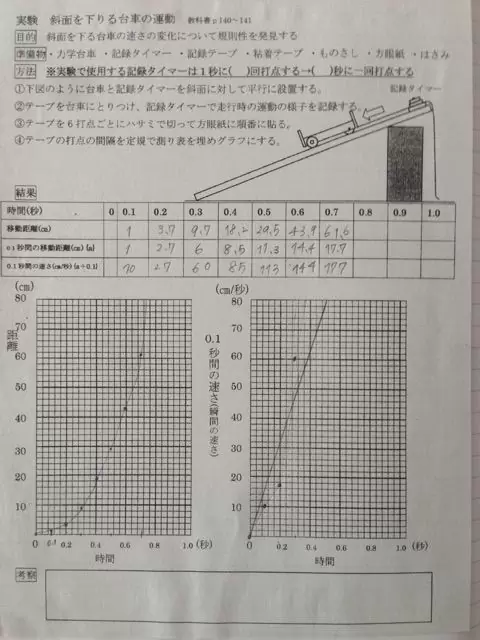



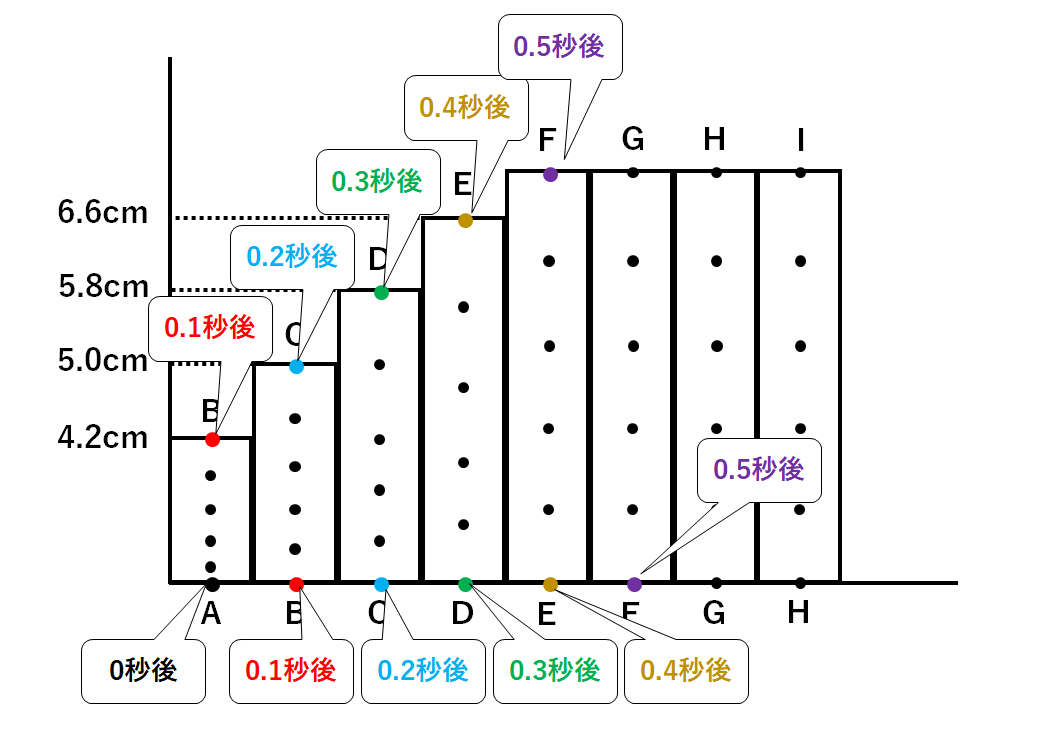
記録タイマーの実験2 ふたばのブログ 理科教育と道徳教育を科学する




平均の速さと瞬間の速さの違いって何 S Tグラフとの関係は 受験物理アイデアの泉
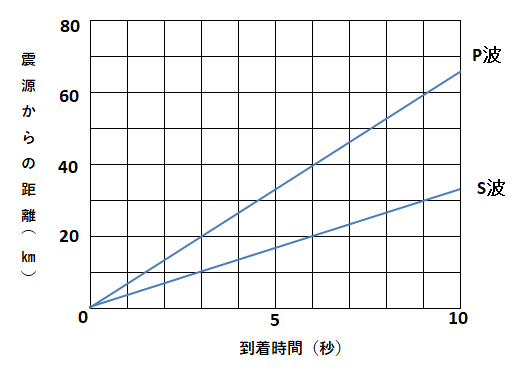



中1理科 地震の波の速さの計算練習問題 デルココ




平均の速度と瞬間の速度 数学ii フリー教材開発コミュニティ Ftext



反応の速さ
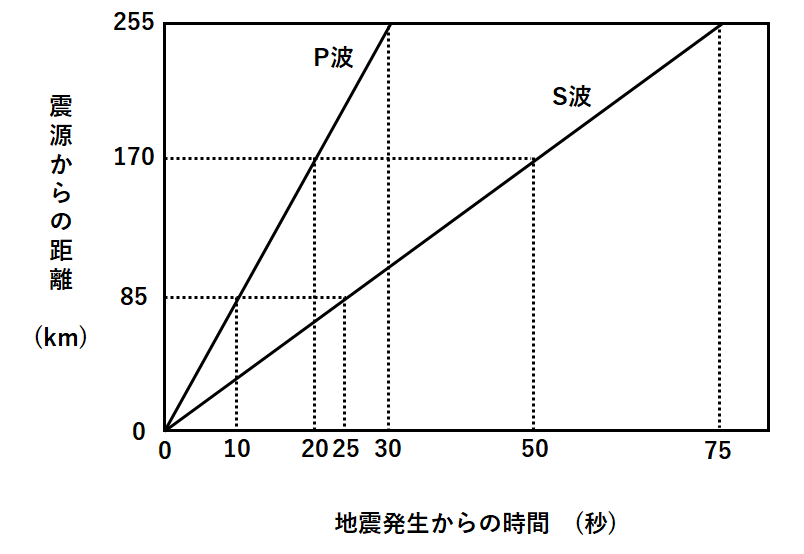



中1地学 地震の計算問題の考え方 中学理科 ポイントまとめと整理




物理基礎 等加速度運動とは何か 公式だけでなくグラフ 平均速度 瞬間速度なども解説 Himokuri
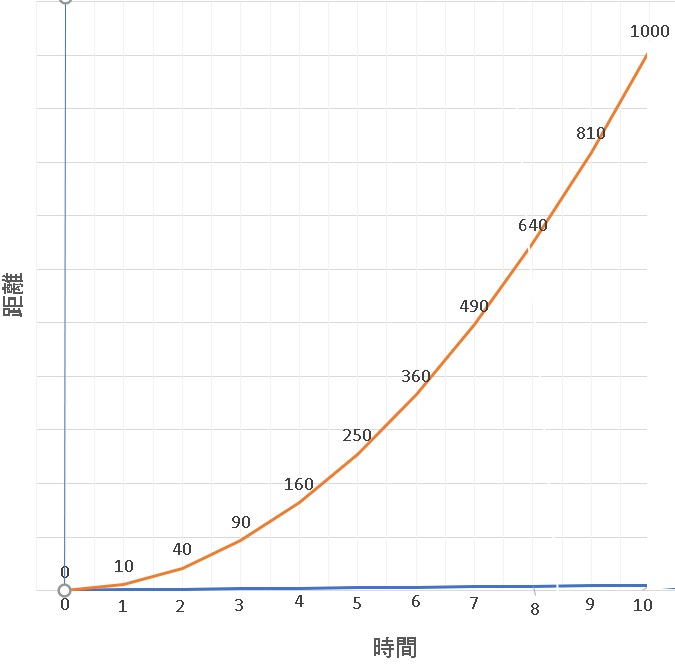



加速度 速度 距離 時間のグラフ面積傾きの意味は 3d Cad Cae 解析と物理の学習まで無料版simulationxpress 使い方入門編




1次関数 時間と道のりの関係を表すグラフ 中学数学 定期テスト対策サイト




中3理科 平均の速さと瞬間の速さ 練習編1 映像授業のtry It トライイット
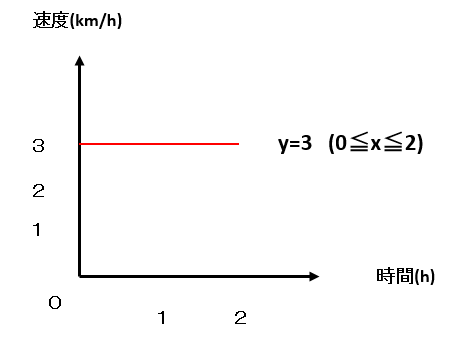



中学数学 距離 速度 時間 を1次関数のグラフを使って理解する 偏差値40プログラマー
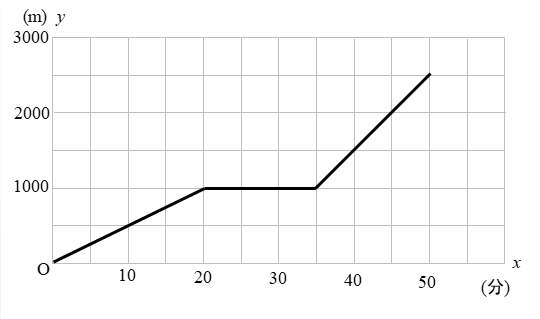



一次関数の利用 追いつく速さの文章問題を解説 数スタ
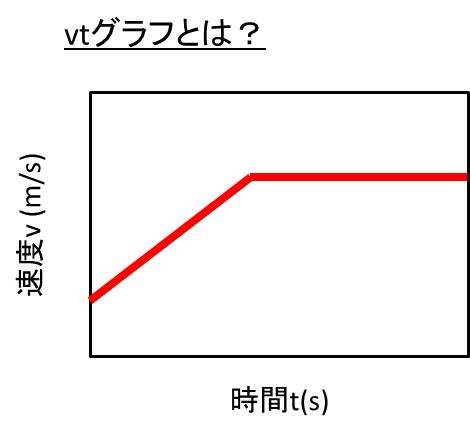



Vtグラフの面積や傾きは何を表す V Tグラフと変位や加速度や速度との関係性は Vtグラフ 速度や時間のグラフ の読み方 ウルトラフリーダム
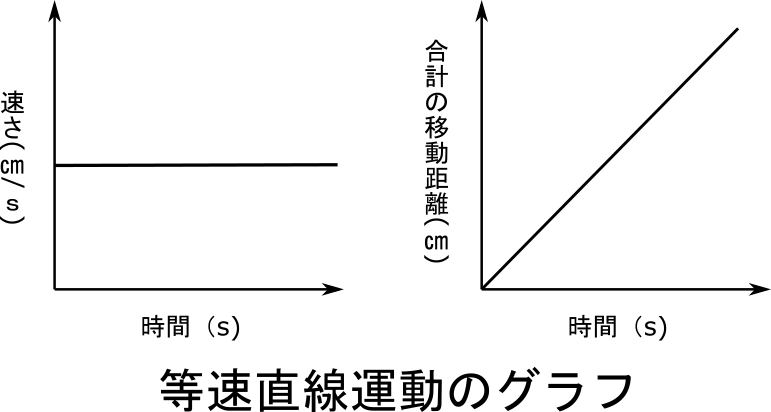



等速直線運動の条件とグラフを理解しよう 理科の授業をふりかえる
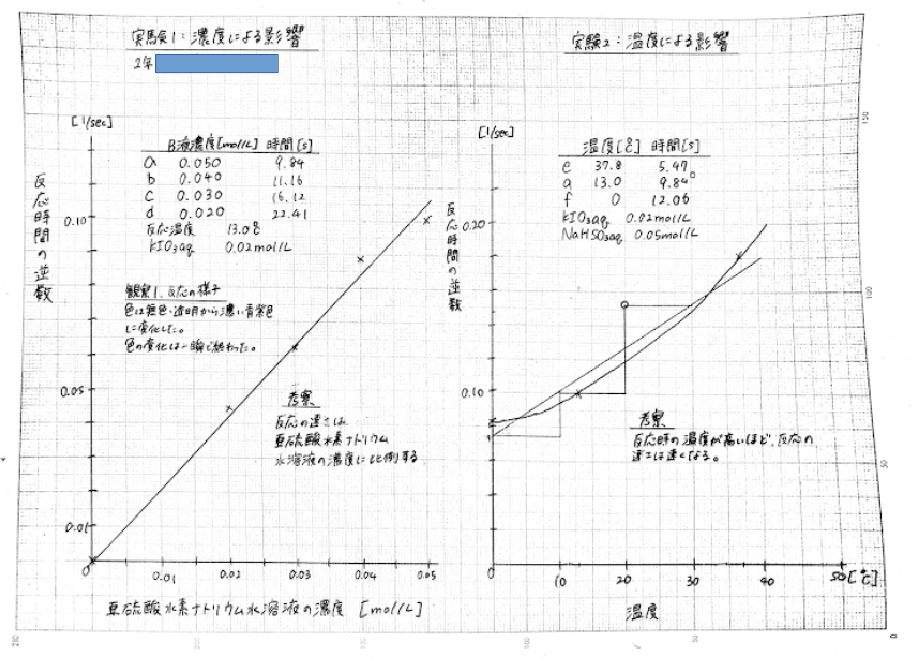



生徒実験 化学反応の速さ レポート 高校化学の教材 分子と結晶模型の ベンゼン屋 楽天ブログ




理科とか苦手で 運動の規則性6 力と運動 3 物体に力が働く運動 斜面を下る運動




速度と加速度 平均と瞬間 高校物理をあきらめる前に 高校物理をあきらめる前に
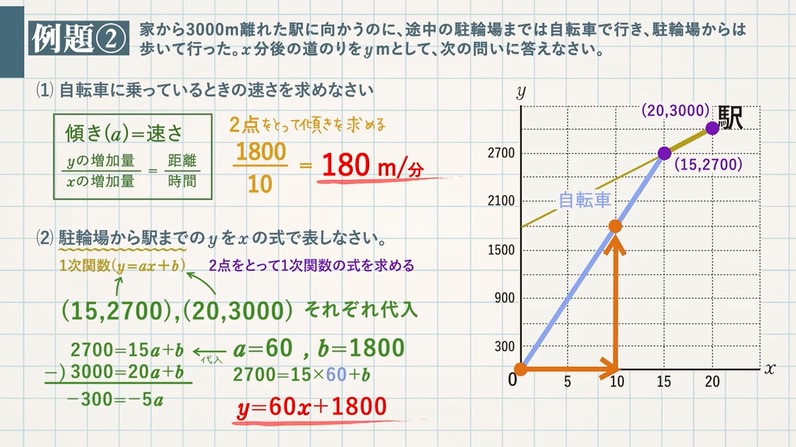



1次関数の速さに関する文章題 距離 速さ 時間 グラフ 教遊者



中3女子です 理科を教えてください 教えへ欲しいのは 3 です 問題文は 図3 Yahoo 知恵袋
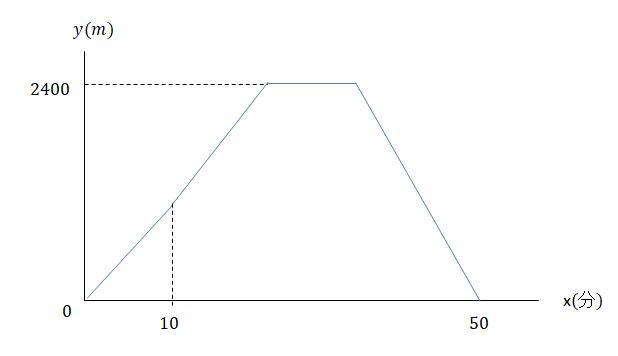



中2数学 一次関数の利用 距離 時間 速さ 定期テスト対策予想問題 デルココ



1



中3物理 いろいろな運動 中学理科 ポイントまとめと整理



中学理科 等速直線運動の実験と計算 なるほどの素



中3物理 速さ 記録タイマー 中学理科 ポイントまとめと整理



加速度 速度 距離 時間のグラフ面積傾きの意味は 3d Cad Cae 解析と物理の学習まで無料版simulationxpress 使い方入門編




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




傾きは速さを表すのではないでしょうか なぜ加速度は傾きで表せるんですか Clearnote




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室



変位と速度と加速度 わかりやすい高校物理の部屋




教えてください 5 と 7 です Clearnote




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室



平均の速度と瞬間の速度の違いとは 公式および求め方




平均の速度と瞬間の速度 数学ii フリー教材開発コミュニティ Ftext
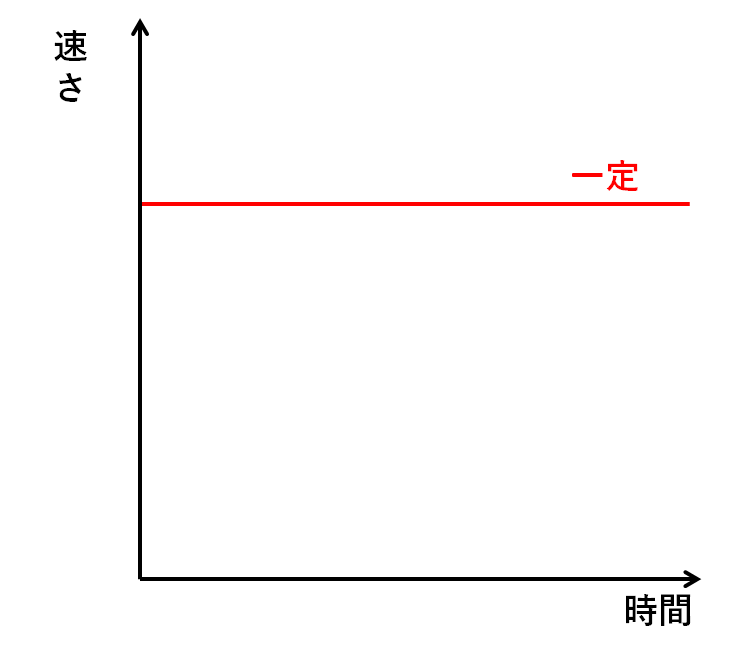



中3物理 いろいろな運動 中学理科 ポイントまとめと整理




Web教材イラスト図版工房 理 17 埼玉 問 05 07




高校物理 x tグラフ 映像授業のtry It トライイット




距離と時間の関係でこのようなグラフの形の場合 それぞれどんな増え方をしている Clearnote




中2数学 一次関数の利用 文章題 歩く距離と時速のグラフ問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト



地震のグラフの読みとり
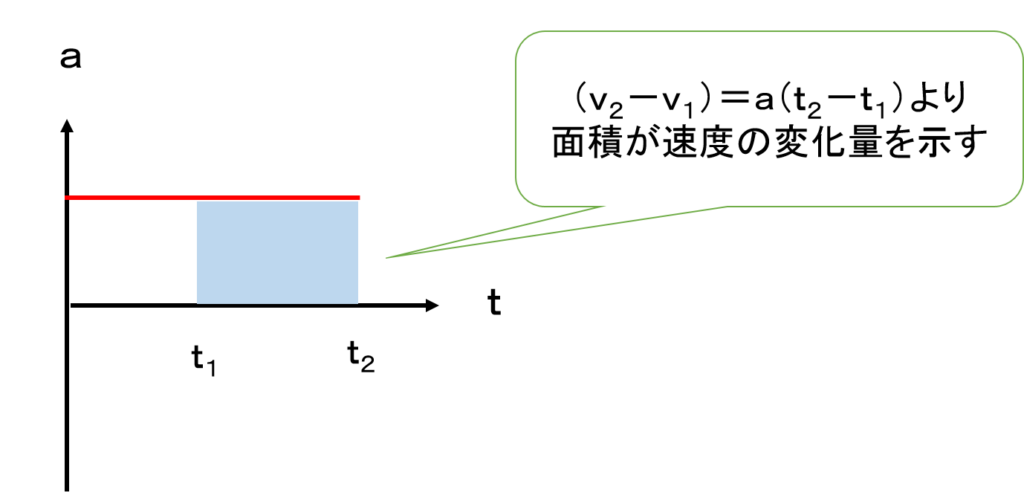



a tグラフ v tグラフやx tグラフに書き直してみよう 平川ブログ




速さと運動 Ict教材eboard イーボード




中2 受験生 一次関数 1次関数の速さに関する文章題 距離 速さ 時間 グラフ 修正版 デジタル板書データ Youtube
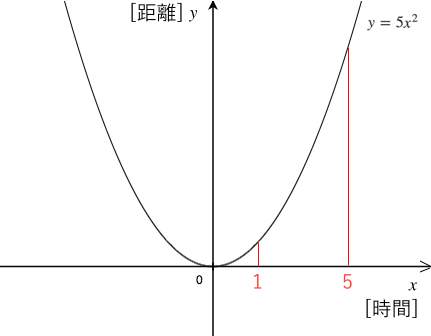



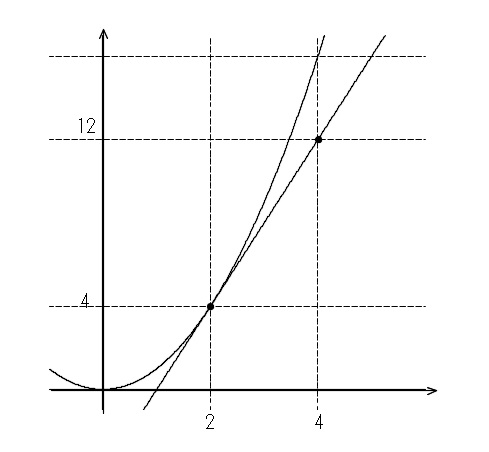
二次関数の利用 平均の速さ 苦手な数学を簡単に




Web教材イラスト図版工房 R C1m 運動する台車の時間と速さのグラフ 1



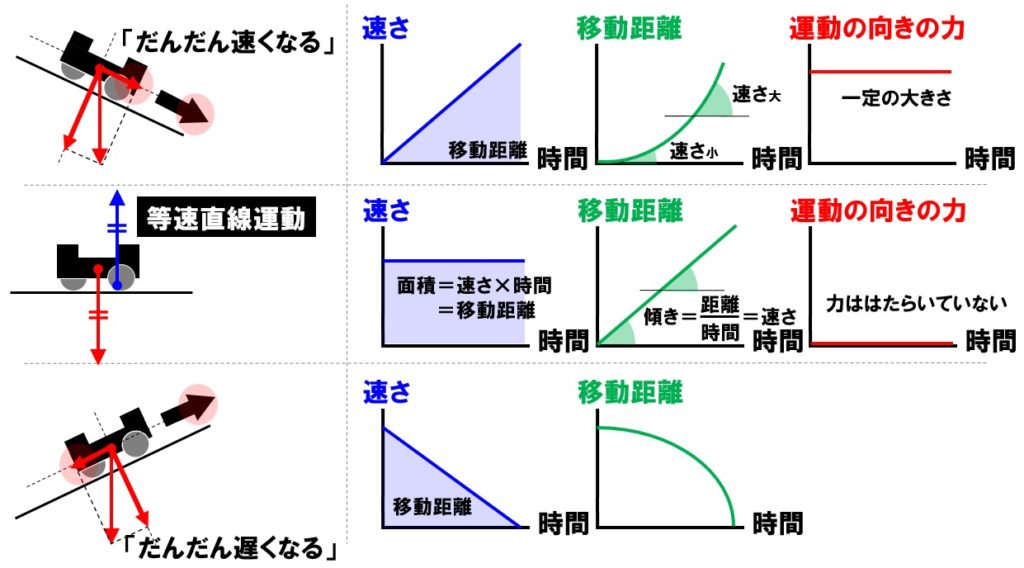
Web教材イラスト図版工房 理 17 東京 K 06 02




平均の速さと瞬間の速さの違いって何 S Tグラフとの関係は 受験物理アイデアの泉



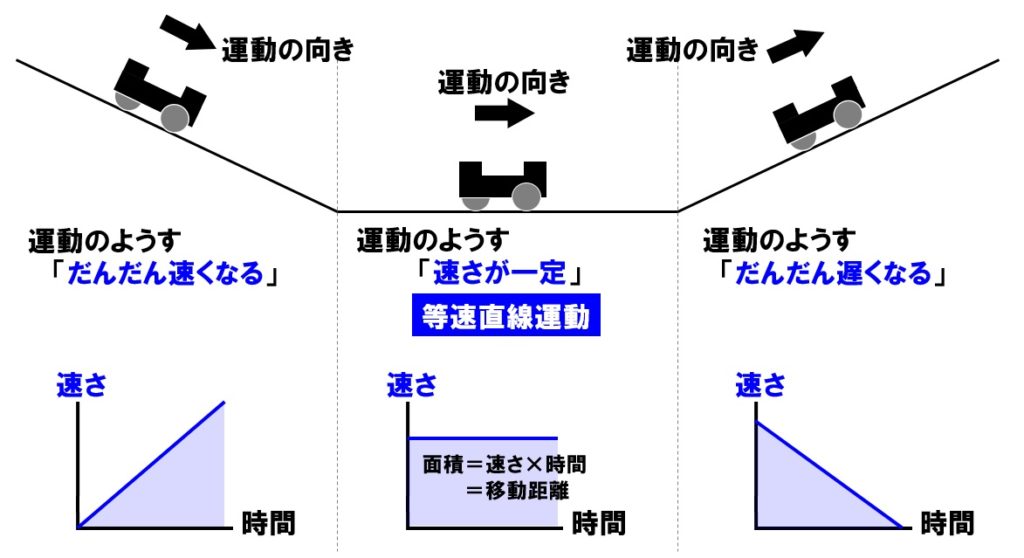
Web教材イラスト図版工房 理 18 高知 A K 02 01



表とグラフ 中学受験ー算数解き方ポータル



グラフから速さを求める 中学から数学だいすき



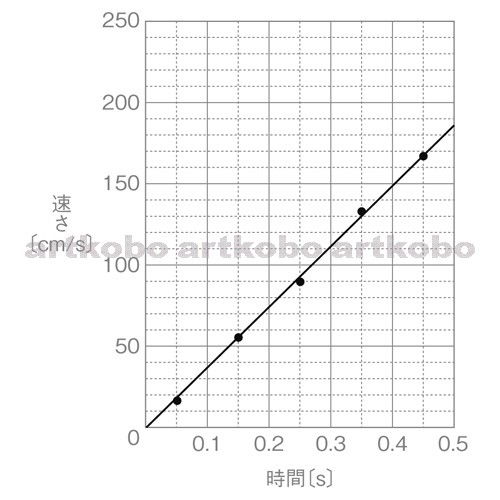
中3理科 台車の運動のポイント Examee



Eラーニング1週目 立川市立第四中学校



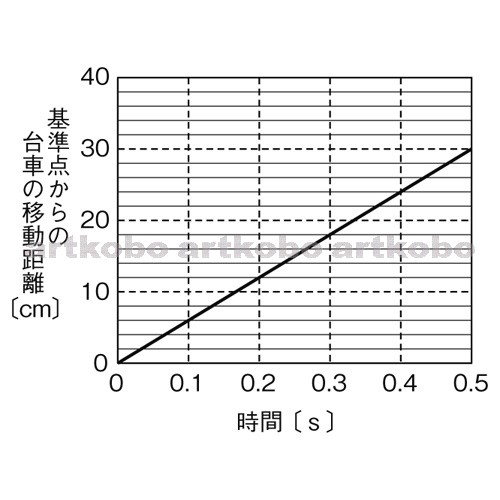
中3理科 台車の運動のポイント Examee




物体の運動



加速度 速度 距離 時間のグラフ面積傾きの意味は 3d Cad Cae 解析と物理の学習まで無料版simulationxpress 使い方入門編



Science 運動 エネルギーの発展問題 2 落下運動 働きアリ




微分積分を速度と距離の関係で理解する 自然科学研究会2 生活の中の数学 その2



速さとグラフ問題より 時間と速度の関係グラフ 立教女学院中学 2010年 中学入試算数68分野別解法



新潟県公立高校入試問題 中3理科の問題集



等速直線運動のグラフ 高校物理をあきらめる前に 高校物理をあきらめる前に



Web教材イラスト図版工房 理 16 千葉 後 問 04 07
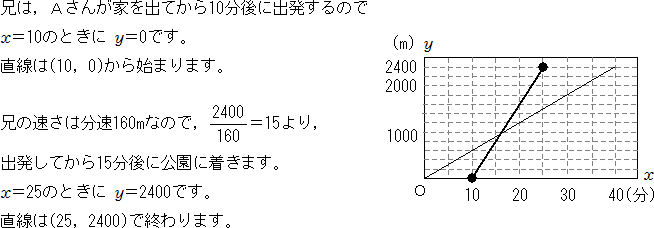



1次関数 時間と道のりの関係を表すグラフ 中学数学 定期テスト対策サイト



速さの求め方




高校物理 仕事wと仕事率p F Xグラフ 仕事率pと速さvの関係 受験の月




等速直線運動公式 グラフの書き方が中学生でもわかる記事 高校生向け受験応援メディア 受験のミカタ



微分を使って瞬間の速さを求めよう 木倍川物理部 キマシスタ
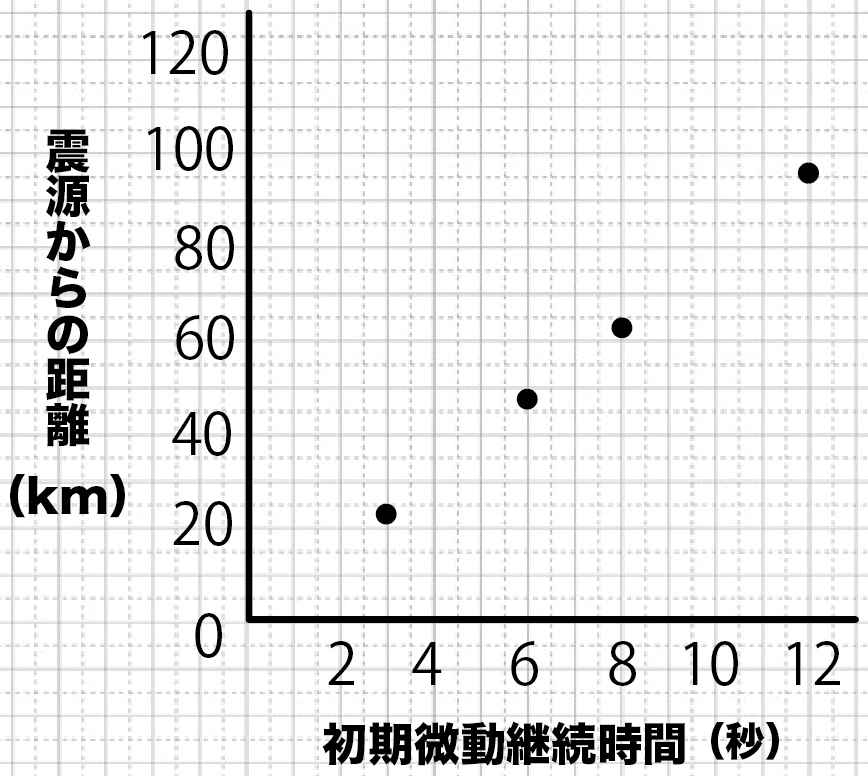



3分で計算できる 初期微動継続時間 震源までの距離 地震発生時刻の求め方 Qikeru 学びを楽しくわかりやすく
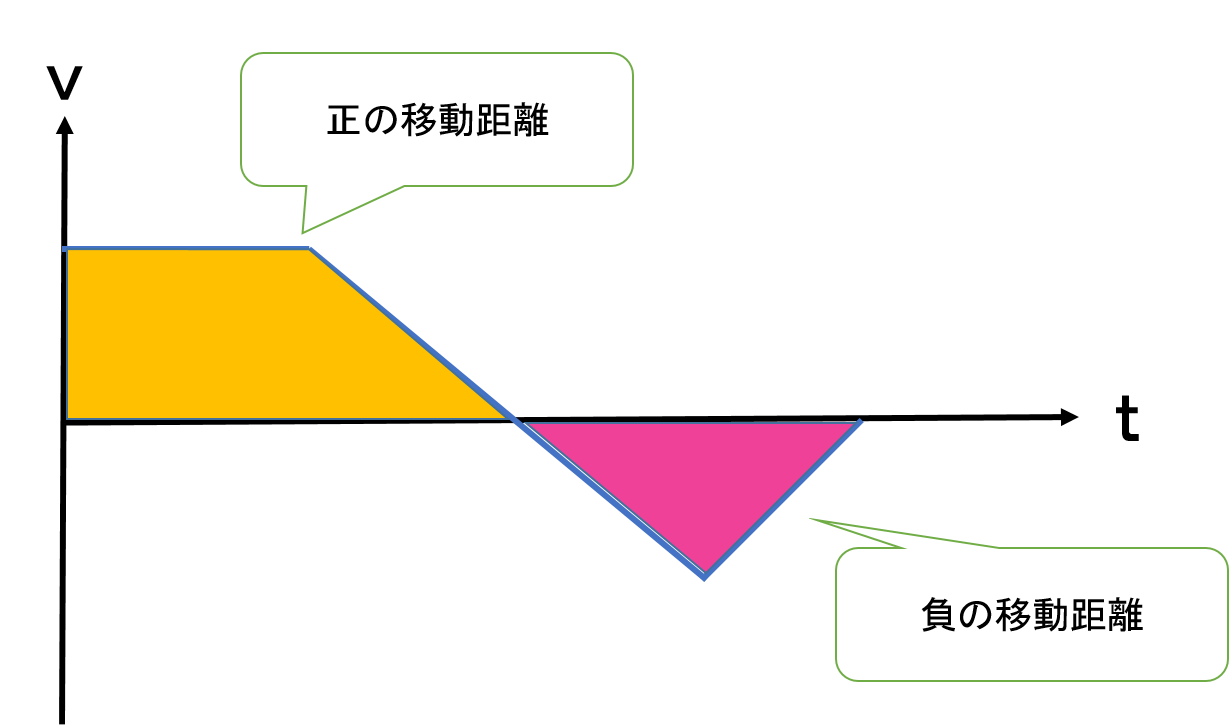



x tグラフとv tグラフ 傾き 面積などの書いてあるグラフの注意点を学ぼう 平川ブログ
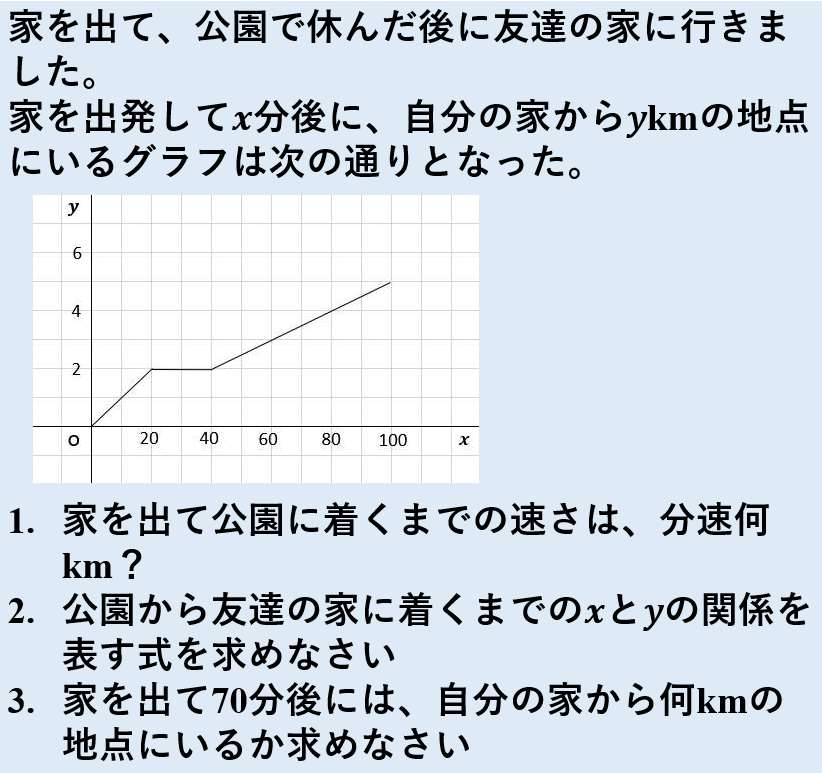



中2数学 一次関数の利用 文章題 歩く距離と時速のグラフ問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




平均の速度と瞬間の速度の違い 速度がわかるx Tグラフ Dr あゆみの物理教室




理科の運動の単元で速さと時間の関係をグラフで表したものがあると思うのですが Clearnote



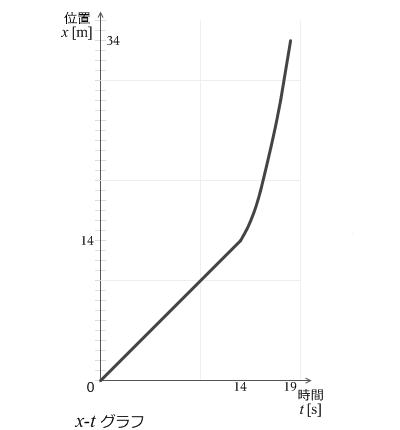
中3物理なぜ 時間と速さは比例関係にあるのに移動距離は二次関数のようなグ Yahoo 知恵袋




物理 等加速度直線運動について 秋田でアクティブに活動



0 件のコメント:
コメントを投稿